Data Visualization Course

Assignment: Test a Multiple Regression Model

08 Nov 2016

Program and outputs

Data loading and cleaning

import numpy as np
import pandas as pandas
import seaborn
import statsmodels.api as sm
import statsmodels.formula.api as smf
from matplotlib import pyplot as plt

data = pandas.read_csv('gapminder.csv')
print('Total number of countries: {0}'.format(len(data)))

Total number of countries: 213

data['alcconsumption'] = pandas.to_numeric(data['alcconsumption'], errors='coerce')
data['femaleemployrate'] = pandas.to_numeric(data['femaleemployrate'], errors='coerce')
data['employrate'] = pandas.to_numeric(data['employrate'], errors='coerce')

sub1 = data[['alcconsumption', 'femaleemployrate', 'employrate']].dropna()
print('Total remaining countries: {0}'.format(len(sub1)))

Total remaining countries: 162

# Center quantitative IVs for regression analysis
sub1['femaleemployrate_c'] = sub1['femaleemployrate'] - sub1['femaleemployrate'].mean()
sub1['employrate_c'] = sub1['employrate'] - sub1['employrate'].mean()
sub1[['femaleemployrate_c', 'employrate_c']].mean()

femaleemployrate_c    2.434267e-15
employrate_c          3.640435e-15
dtype: float64

Single regression

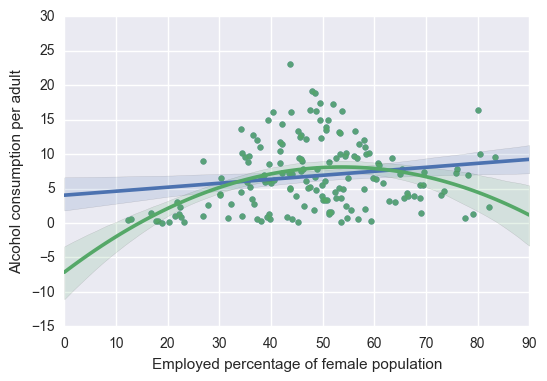
# First order (linear) scatterplot
scat1 = seaborn.regplot(x='femaleemployrate', y='alcconsumption', scatter=True, data=sub1)

# Second order (polynomial) scatterplot
scat1 = seaborn.regplot(x='femaleemployrate', y='alcconsumption', scatter=True, order=2, data=sub1)
plt.xlabel('Employed percentage of female population')
plt.ylabel('Alcohol consumption per adult')
plt.show()

png

# Linear regression analysis
reg1 = smf.ols('alcconsumption ~ femaleemployrate_c', data=sub1).fit()
reg1.summary()
OLS Regression Results
Dep. Variable: alcconsumption R-squared: 0.029
Model: OLS Adj. R-squared: 0.023
Method: Least Squares F-statistic: 4.787
Date: Tue, 08 Nov 2016 Prob (F-statistic): 0.0301
Time: 11:20:44 Log-Likelihood: -487.57
No. Observations: 162 AIC: 979.1
Df Residuals: 160 BIC: 985.3
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [95.0% Conf. Int.]
Intercept 6.8124 0.388 17.559 0.000 6.046 7.579
femaleemployrate_c 0.0578 0.026 2.188 0.030 0.006 0.110
Omnibus: 12.411 Durbin-Watson: 1.915
Prob(Omnibus): 0.002 Jarque-Bera (JB): 13.772
Skew: 0.713 Prob(JB): 0.00102
Kurtosis: 2.909 Cond. No. 14.7 
# Quadratic (polynomial) regression analysis
reg2 = smf.ols('alcconsumption ~ femaleemployrate_c + I(femaleemployrate_c**2)', data=sub1).fit()
reg2.summary()
OLS Regression Results
Dep. Variable: alcconsumption R-squared: 0.135
Model: OLS Adj. R-squared: 0.125
Method: Least Squares F-statistic: 12.45
Date: Tue, 08 Nov 2016 Prob (F-statistic): 9.45e-06
Time: 11:20:45 Log-Likelihood: -478.17
No. Observations: 162 AIC: 962.3
Df Residuals: 159 BIC: 971.6
Df Model: 2
Covariance Type: nonrobust
coef std err t P>|t| [95.0% Conf. Int.]
Intercept 7.9540 0.449 17.720 0.000 7.067 8.840
femaleemployrate_c 0.0605 0.025 2.419 0.017 0.011 0.110
I(femaleemployrate_c ** 2) -0.0053 0.001 -4.423 0.000 -0.008 -0.003
Omnibus: 9.022 Durbin-Watson: 1.930
Prob(Omnibus): 0.011 Jarque-Bera (JB): 9.369
Skew: 0.589 Prob(JB): 0.00924
Kurtosis: 3.024 Cond. No. 459.

Multiple Regression

# Controlling for total employment rate
reg3 = smf.ols('alcconsumption ~ femaleemployrate_c + I(femaleemployrate_c**2) + employrate_c', data=sub1).fit()
reg3.summary()
OLS Regression Results
Dep. Variable: alcconsumption R-squared: 0.345
Model: OLS Adj. R-squared: 0.333
Method: Least Squares F-statistic: 27.79
Date: Tue, 08 Nov 2016 Prob (F-statistic): 1.73e-14
Time: 11:20:46 Log-Likelihood: -455.63
No. Observations: 162 AIC: 919.3
Df Residuals: 158 BIC: 931.6
Df Model: 3
Covariance Type: nonrobust
coef std err t P>|t| [95.0% Conf. Int.]
Intercept 7.5561 0.396 19.092 0.000 6.774 8.338
femaleemployrate_c 0.3312 0.044 7.553 0.000 0.245 0.418
I(femaleemployrate_c ** 2) -0.0034 0.001 -3.204 0.002 -0.006 -0.001
employrate_c -0.4481 0.063 -7.119 0.000 -0.572 -0.324
Omnibus: 2.239 Durbin-Watson: 1.862
Prob(Omnibus): 0.326 Jarque-Bera (JB): 1.788
Skew: 0.205 Prob(JB): 0.409
Kurtosis: 3.311 Cond. No. 463. 
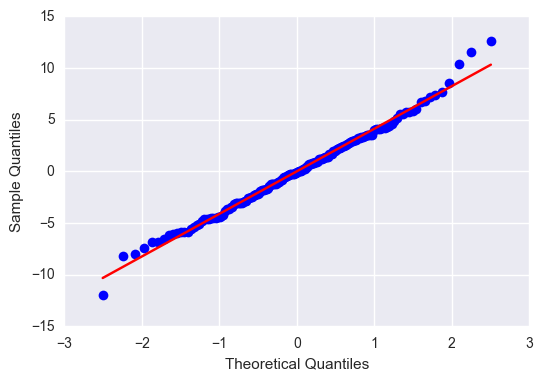
#Q-Q plot for normality
sm.qqplot(reg3.resid, line='r')
plt.show()

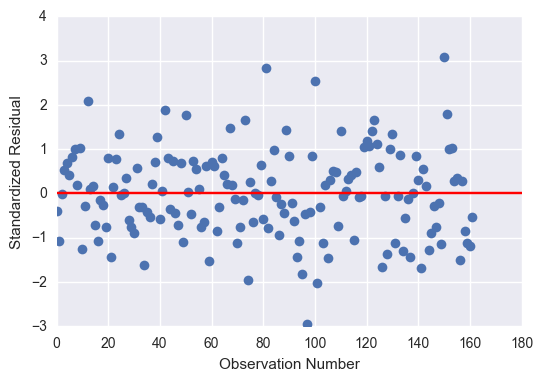
# simple plot of residuals
stdres = pandas.DataFrame(reg3.resid_pearson)
plt.plot(stdres, 'o', ls='None')
l = plt.axhline(y=0, color='r')
plt.ylabel('Standardized Residual')
plt.xlabel('Observation Number')
plt.show()

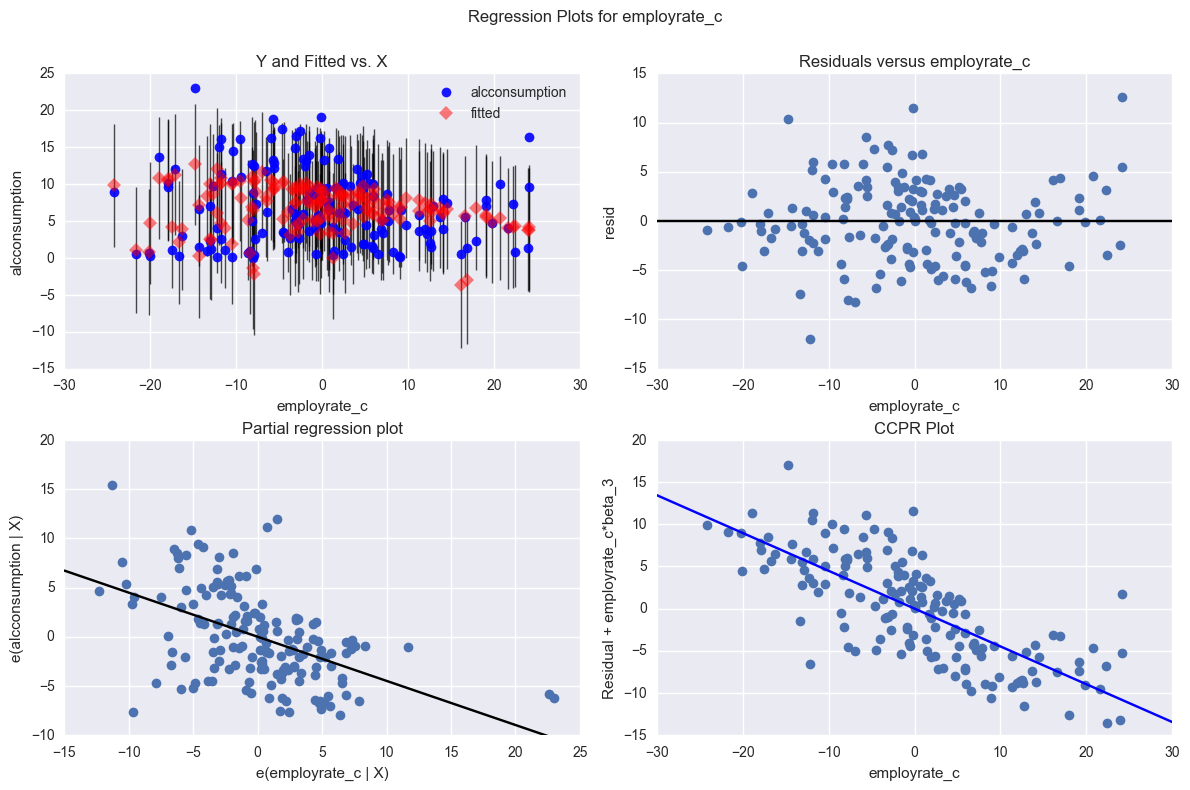
# additional regression diagnostic plots
fig2 = plt.figure(figsize=(12,8))
sm.graphics.plot_regress_exog(reg3,  "employrate_c", fig=fig2)
plt.show()

# leverage plot
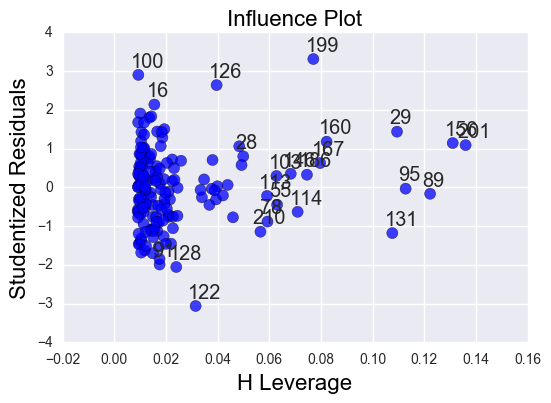
sm.graphics.influence_plot(reg3, size=8)
plt.show()

png

png

png

png

Summary

I started by analyzing the effect on female employment rate on alcohol consumption per adult. I found a significant (p = 0.0301) positive (coef = 0.0578) effect that explained a very small (r-squared = 0.029) portion of the data.

I then added a polynomial regression for female employment rate. I found a more significant (p = 9.45e-06) effect that explained a larger (r-squared = 0.135) portion of the data. Both of the variables individually are significant (p = 0.017 and p < 0.001) which confirms that the best fit line includes some curvature.

Assuming that the general employment rate would have an effect on the female employment rate, I decided to run my multiple regression, correcting for total employment rate. Again, my results were more significant (p = 1.73e-14) and had a greater effect (r-squared = 0.345). Again, all my variables were individually significant (p < 0.001, p = 0.002, p < 0.001).

Despite the overall significance of my explanatory variables, the total effect size was only 35%, so there are a fair number of residuals outside of 1 and 2 standard deviations. Nonetheless, the residuals with the greatest leverage were within 2 standard deviations, so I am confident saying that female employment rate, independent of the total employment rate, has a significant effect on alcohol consumption.

Related Posts